Writing a Stronger Minesweeper-Engine in C++
Originally published on LinkedIn on August 30, 2020
At the end of my previous post, I outlined how one could potentially improve the Minesweeper-engine to make sensible decisions if no cell is ensured to be safe based on the simple deduction rules we looked at.
This article will cover some aspects of a solver written in C++:
Comparing the speed of the naïve previous algorithm‘s Python and C++ implementation
Some notes on the C++ implementation, e.g. parallelism and thread safety
Using simple depth first searches to devise a stronger solving algorithm
Comparing the win rate of the naïve algorithm to the stronger one
An analysis of the game difficulty in terms of mine density
The implementation details are described in a bit more technical terms than in previous articles, but the utilized algorithms are easy. The code is linked to on GitHub, and for visualization, this neat and lightweight engine was used.
Introduction
To recap, the question is how to decide on which cell to click once the simple deduction rules from before are no longer sufficient. One very naïve method was implemented based on each imposed constraint B on a neighbouring unclicked cell C, where B is any clicked cell revealing the number of neighbouring mines.
For example, a clicked cell revealing the number 1 and having exactly 8 unclicked neighbours, each neighbour would have an estimate of 12.5% - there must be exactly 1 mine amongst 8 cells. If there are only 3 neighbours, then each is assigned a probability of 33.3%.
Generally, a naïve formula is the following, and the engine would pick the minimum over all C:
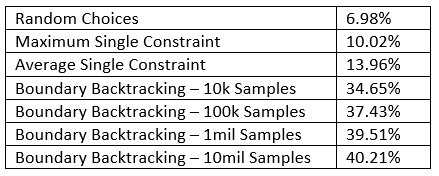
Cells without constraints are assigned a default probability based on the number of remaining mines and unclicked cells. Let us denote this the maximum single constraint algorithm. Whilst this improved the win rate versus purely random choices from 7% to 10% on "Expert", we can do a lot better once we succeed in jointly considering all constraints.
An intermediate step was replacing the “max” in the above formula with “mean”, i.e. averaging over all constraints on a cell. This, to no surprise, only improved play strength marginally to 14%.
The much more powerful method will single out the boundary, defined as all cells that have already been clicked and hence impose constraints by revealing the number of neighbouring mines, as well as these neighbouring constrained cells. Define a configuration to be a distribution of mines that satisfies these constraints. Then, for each constrained cell C, it will estimate the amount of all configurations along the boundary where C is a mine divided by the entire number of configurations. This quotient yields a probability estimate for each cell C, and hence we will be able to decide which one of these cells to click (or whether to click a completely unconstrained cell away from the boundary!).
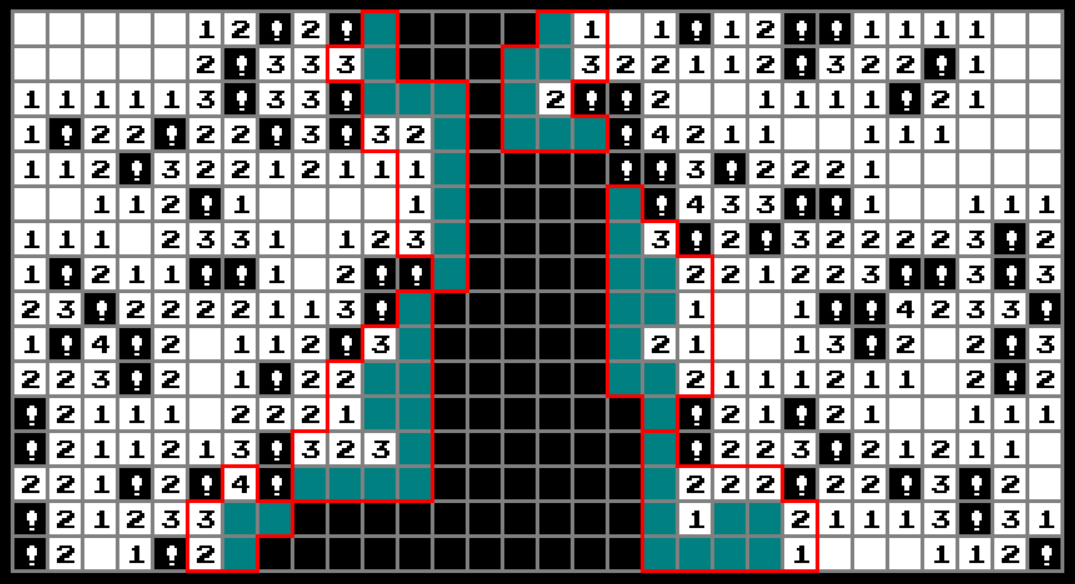
To visualize this process, consider the below game state, with the constrained cells along the boundary highlighted in cyan. These cells as well as the boundary are demarcated by red lines; Note that – and this is essential for an efficient implementation – there are 6 connected components which can be solved individually; These components are segregated by virtue of not having a common constraint.
For a trivial example,, in the bottom left corner, there are three constrained cells marked in cyan, and the boundary labels “2”, “3”, “4” degenerate to “1”, “1”,”1” taking into account the flagged known mines. There are exactly two possible configurations that satisfy these constraints:
One mine on the top left
Two mines – one on the bottom left cell, one on the top right cell.
This is a case in which we can fully compute the outcome. However, the boundary can grow large in some situations, so I prune the breadth of the search tree in practice. An obvious upper bound for the number of configurations along the boundary is 2^N, with N being the number of cyan coloured cells per component.
Note also that there is a major difference to the method I alluded to at the end of my previous post. There, I suggested sampling configurations across the entire game board and checking whether such a sample is valid. This turns out to be a bad idea – the reason being the sheer size of the configuration space of mines. And why should we sample mines on cells where this not even a constraint to check against? Hence, we will at first only look at the boundary, which significantly reduces the space to consider. As we reach an endgame state with less “black space”, the number of remaining mines away from the boundary starts to matter more as the configuration space shrinks. As you perhaps see already, the unconstrained cells influence our probability estimates. I will come back to this point when we introduce a simple adjustment term to account for these off-boundary cells.
Now, the configuration space along the boundary will still be rather large in some cases, so efficiency matters.
A speed comparison (apples and oranges)
Let us first consider the naïve "maximum constraint" method. My initial Python implementation took on average 0.45 seconds per game on “Intermediate” difficulty, while the C++ implementation took 0.00127 seconds.
Phrased differently, that means about 2 games per second versus about 800 games per second.
This is a somewhat unfair comparison given that my Python implementation was not written with speed in mind. The goal was to quickly solve this CS50 project and test it out. For one, I started by using lists as data structures to represent board states, and inclusion tests were performed by means of type conversions to sets every single time and using the issubset()-method. That is written quick and dirty – it works, but it is far from optimal.
Now, the non-primitive data types that are used in the C++ implementation to do computations on the game state are primarily arrays and vectors, both of which can be extremely runtime efficient if used properly. Sticking with the above example, my C++ implementation of checking whether A contains B isn’t exactly fast either given its quadratic complexity which can be brought down to O(|B|*log|A|) using std::set as an alternative data structure. Moreover, once we know that A indeed contains B, std::set_difference(A, B) returns the complement A\B in linear complexity. These are some improvements I can still make, and if you are interested in an overview of the utility of the Standard Template Library, this presentation (by a lead Murex developer!) is hugely informative.
Speaking of the STL, I also experimented with std::vector::reserve in an attempt to reduce costly memory allocations. However, there was very little yield, if any at all, from doing so since the size of the vectors I dealt with were usually unpredictable. Moreover, std::vector::push_back has constant amortized complexity, so it is usually good enough for cases where several sequential additions are made.
Since we mentioned arrays, one more note on the topic of storage: A well-known technique to improve tight loops is to avoid representing two-dimensional data, like the game board, as a pointer of pointers, and instead to map it into one dimension via the indexation formula x + y*width. This trades potential memory fragmentation for locality due to allocation into a continuous block of memory and is hence cache friendly. Of course, one can avoid arrays of raw pointers completely in modern C++ in the first place, circling back to the topic of vectors.
Another major source of performance gain is multithreading, or in this case, separating the game’s interface from engine calculations. This concept introduces some complexity on its own right, see the next section; Nevertheless, it is always a good idea to search for parallelizable parts of an application. My Python-script does all the work in a single thread.
So, the main three basic lessons I learned were “leverage the STL where possible”, “understand the data structures I use”, and “understand my instruction flows”.
None of these tangential observations replace a fully-fledged code review and runtime profiling using the debugger of choice. Once I do these, some more optimizations will likely stand out. In terms of the logical structure of the program, persistent storage of the boundary would likely be faster than a build-up each time the engine is called to make a move, for example. In terms of the actual implementation, a beginner like me should be wary when trying to come up with supposedly obvious fixes, since the compiler is usually hard to outsmart.
A note on parallelism and thread safety (MUTual EXclusion, or std::mutex)
Whenever a lot of work needs to be done but the user should still be allowed to a) see what is going on or to b) intervene (for example, by interrupting the computation), it is generally a good choice to multithread. Moreover, this may bring forth a performance advantage by utilizing modern CPU architecture.
In this program, as mentioned before, the computation of a move is segregated from the drawing and user input handling routines, meaning that the user does not have to stare at a frozen screen while the engine does its job.
Spawning a new thread and making subroutines run in parallel is made easy in C++ using the std::thread class since the standard library and the scheduler of the operating system do the heavy lifting. However, one major point I needed to think about was ensuring thread safety, a concept which is designed to eliminate unintended interactions between threads.
Consider the following: The engine stores its current state in several vectors. Now, my drawing routine reads these and draws a representation of the engine internals to the user. What can happen if the drawing thread cycles through one of these vectors, while the engine thread makes modifications to the same by altering or deleting elements? An access violation and hence a crashed program. This is a mere annoyance for a game but could be devastating for critical systems.
Thankfully, the C++ STL provides methods of synchronisation. From cppreference: „The mutex class is a synchronization primitive that can be used to protect shared data from being simultaneously accessed by multiple threads.“.
The implementation is simple – Both threads need to share a mutex-instance and they will need to wait for it to be unlocked, as needed, while the other thread does its job. Of course, the instruction flow must be designed in a way to avoid deadlocks; The thread owning a mutex should ensure to unlock it again!
Moreover, and this is extremely important, any form of synchronization decreases parallelism and hence performance. If the latter is crucial, then other concepts to ensure thread safety are typically better suited (see also atomic operations).
With all of that out of the way, we continue with the less technical part.
The boundary backtracking algorithm (applying brute force)
The algorithm is easy as it can be constructed using two very fundamental graph operations – dividing the boundary into its connected components and performing depth first searches along the boundary components to find a subset of all permissible mine configurations. This process was already described in the introduction, but here is a more detailed summary followed by two key observations:
Find the boundary and all neighbouring constrained cells
Segregate the boundary and the constrained neighbours into connected components. Two unclicked cells are defined to belong to the same connected component if they share a common boundary cell.
For each connected component, with boundary cells B1, …, Bm and constrained cells C1, …, Cn:
Simulate C1 as being a mine and see if the local upper constraints are violated, i.e. if we have set more cells as mines as allowed by the constraints surrounding C1 (This step is here to reduce search complexity). If not, continue recursively with C2 (and then C3, etc.).
Once the recursive search returns, simulate C1 as not being a mine and continue recursively with C2 (C3, etc.).
If we arrive at Cn at the end of the recursion, check if the entire set of constraints by B1, …, Bm are satisfied. If they are, we have found a permissible configuration, and a counter is increased for each Ci which we have simulated as a mine.
If at any time in this recursive search the number of sampled configurations exceeds a pre-set threshold, we terminate.
This illustrates the recursive search along the uppermost connected component.
Lastly, once this backtracking search is completed for all components:
Calculate probabilities based on the sampled configurations via (#configurations where C is a mine) / (#total configurations). For unconstrained cells away from the boundary, set a default probability as (#remaining mines) / (#unclicked cells).
Pick the cell with the lowest probability.
We are not quite done yet as there are two further modifications to be aware of.
Firstly, if the boundary size is large relative to the maximum number of samples, the game will likely only sample configurations where the first cell C1 is simulated as a mine (because the search is terminated before reaching the next branch). This means that nearby cells C2, C3 etc. will likely violate the upper constraints, hence the algorithm will not find any configurations where those cells are mines and will consider them safe to click (when they might be far from that!). This is a shortcoming of the depth-first traversal. In the below cropped animation, you can see this in effect: The cell C2 is initially highlighted in green to signal that it is safe, before finally being probed and stabilizing at a 50% probability. If we utilized a lower number of samples, the game would be lost with a 50-50 chance in that turn.
To mitigate this bias, I rotate C1, …, Cn repeatedly (ending up with e.g. C2, C3, …, Cn, C1 in the first step) and perform the backtracking each time with an allocated fraction of samples 1/n. This is akin to an averaging over several traversals, with each cell being guaranteed to be at the top of the tree exactly one time. This is a rather ham-fisted approach, so I am sure that a reader proficient in data structures and algorithms can think of a better solution – if you have one, I would love to hear it!
Secondly, I promised that I would come back to the topic of off-boundary configurations. Look back at this slightly altered example from the beginning and suppose that 2 mines are remaining on a total of 8 unclicked cells.
We found exactly two possible configurations along the cyan-coloured boundary: One comprised of two mines, one comprised of just one mine. In the latter, the one remaining mine must be off-boundary, i.e. on any of the 5 unconstrained cells. This means that, in the probability estimation formula (#configurations where C is a mine) / (#total configurations), the denominator and/or nominator should be increased accordingly – otherwise, the estimate will have a significant error term. In general, this adjustment involves calculating the remaining unconstrained off-boundary configurations using the binomial coefficient nCk, which is only feasible in the endgame unless you like large numbers; e.g. nCk(35,17)= 4.537.567.650 will already produce 32-bit integer overflows. If you can think of a smarter way to adjust the probability estimates, I would be keen on knowing about it.
Win rate analysis
Let us compare the four algorithms we have looked at, each tested over ten thousand games on “Expert” Difficulty (board size 30*16 with 99 mines). As a final step, it would be interesting to see the point of convergence as the sample restriction is lifted.
Game difficulty analysis
Where in the previous section we have held the difficulty constant and varied the algorithm, we will now proceed vice versa. We will consider the boundary sampling algorithm at one million maximum samples and look at win rates over varying difficulties.
Firstly, note that the size of the game board is not all that meaningful aside from the boundary search time; what governs difficulty is the mines per cell, or density. The standard values for width, height and mine count, are:
Beginner: 9x9, 10 mines (density = 0.12347)
Intermediate: 16x16, 40 mines (density = 0.15625)
Expert: 30x16, 99 mines (density = 0.20625)
Plotting the win rate over 10,000 games for varying densities yields the following result, with the three standard difficulties highlighted by vertical bars:
Note that the win rate for “Expert” is, at 37.7%, lower than the 39.51% recorded in the previous section. This suggests that tests over a larger number of games would be necessary to converge to the true mean. The percentage of moves for which the probabilistic engine needed to be invoked (i.e. where the deduction rules from the previous article were insufficient) is also included.
One further parameter of the game, aside from width/height/mine count, is the behaviour of the first click. In the Minesweeper implementation that I programmed in the previous article, and which I replicated here, the first cell is always guaranteed to be a zero. To make the game harder, one can relax this condition and only guarantee the first clicked cell to not be a mine. The situation then changes as follows:
Conclusion
The chosen topics were extremely “hands on”. According to the Wikipedia Article on Minesweeper, the game's solvability has been looked at on a much more sophisticated level, including an analysis of NP completeness. Nevertheless, it is incredibly fun for me to revisit classic games and to solve them using fairly basic methods.
There are surely ways to improve the solver in more dimensions than just computational speed. For instance, if two cells are estimated to have an equal likelihood of containing a mine, which one should be clicked? There is value in the information that a click uncovers - more is better, which means that we should look for cells that are likely to be a "zero", which in turn is a function of the number of neighbouring unclicked cells. This can surely be formalized and molded into an algorithm, but will - again - be left for another day.